
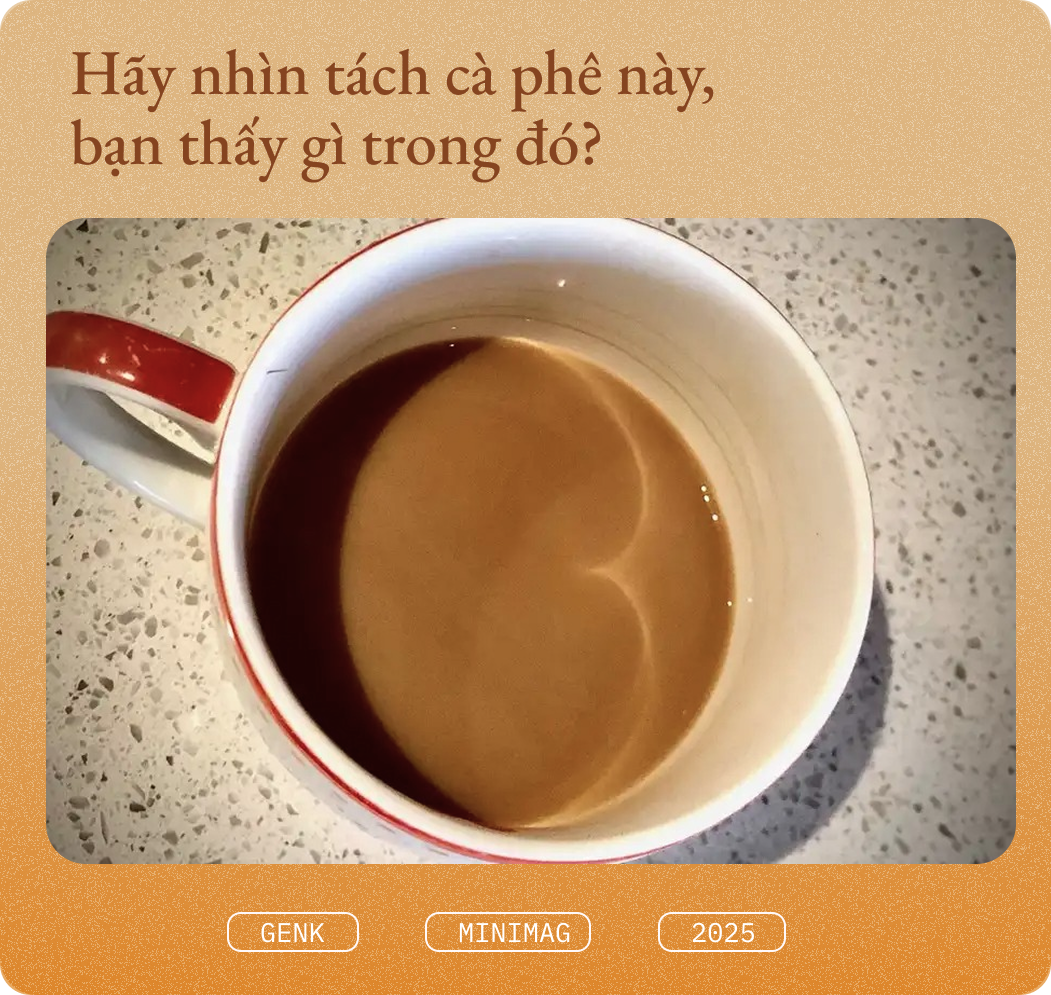
Hãy nhìn tách cà phê này, bạn thấy gì trong đó? Những vệt khói sáng màu có vẻ như là bọt sữa Latte Art đang tạo thành hình trái tim. Nhiều người có thể tưởng tượng ra đó là một quả táo, hay thậm chí… một cái mông.
Nhưng nếu bạn học toán đủ sâu, một nhà toán học khi nhìn vào "cái mông" này sẽ biết: Đó không phải là tác phẩm của một barista hay nghệ sĩ tạo hình cà phê bằng sữa nào cả.
Chắc chắn, trên đời không ai có thể vẽ ra hình một trái tim tròn đều và hoàn hảo đến vậy - bằng tay. Ngay cả khi có một barista có thể làm được điều đó đi chăng nữa, anh ta cũng không thể may mắn hết lần này đến lần khác:

Trên internet có đầy rẫy ảnh chụp những tách cà phê hình cái mông như thế này, trong đủ mọi nền văn hóa khác nhau từ Mỹ, Pháp, Đức cho đến Isreal và cả Ấn Độ. Ở Trung Quốc, những cái mông này xuất hiện trong cả tách trà.
Chẳng lẽ, trên đời lại có nhiều barista và nghệ nhân đạo trà đỉnh cao đến vậy?

Mặt Trời luôn mọc ở hướng đông, ở Mỹ cũng như ở Việt Nam. Nước sôi ở 100 độ C, ở xích đạo cũng như ở Nam Cực. Mọi thứ đều sẽ rơi xuống đất, ở Trái Đất cũng như trên Sao Hỏa. Hóa ra, những cốc cà phê hình cái mông cũng vậy.
Như triết gia người Áo Karl Popper từng viết vào năm 1934, trong cuốn sách kinh điển của ông "Logic của khám phá khoa học": "Những sự kiện đơn lẻ không thể tái lập thì không có ý nghĩa gì đối với khoa học".
Nếu Isaac Newton thả một quả táo và nó rơi xuống đất, còn cây táo nhà hàng xóm Newton lại rụng quả ngược lên trời, nhân loại sẽ vĩnh viễn không bao giờ có Định luật vạn vật hấp dẫn.
Nếu nhà vật lý người Anh Arthur Eddington không quan sát thấy ánh sáng đến từ các ngôi sao bị bẻ cong khi đi qua Mặt Trời, trong sự kiện nhật thực vào năm 1919, và William Campbell không lặp lại được thí nghiệm đó tại Úc vào năm 1922, thuyết tương đối rộng của Albert Einstein sẽ vẫn chỉ là một tin đồn từ đầu ngõ đến cuối ngõ.

Tương tự, việc một thầy bói chẳng may đoán trúng được một vài sự kiện, nhưng thất bại trong việc đoán đúng các sự kiện khác thì khả năng tiên tri của họ không bao giờ được công nhận.
Nó cũng giống như thí nghiệm ngoại cảm nổi tiếng của nhà tâm lý học người Mỹ Joseph Banks Rhine tại Đại học Duke năm 1930. Trong đó, ông tuyên bố một nhóm nhà ngoại cảm ở một căn phòng này có thể đoán được một người khác, đang ở trong một căn phòng khác, vừa chọn lá bài nào.
Nếu không có khả năng ngoại cảm, xác suất đoán đúng ngẫu nhiên của 1 trong 5 lá bài chỉ là 20%. Nhưng Rhine đã thực sự tìm ra được một nhóm người có xác suất đoán đúng gấp đôi, 40%, và tuyên bố họ là những nhà ngoại cảm.
Thật không may, thí nghiệm của Rhine đã không bao giờ được lặp lại bởi bất cứ nhà khoa học nào trên thế giới, với bất kỳ nhà ngoại cảm nào kể năm 1930 tới nay. Vì vậy, khả năng ngoại cảm vẫn được coi là phi khoa học.

Tóm lại, những sự kiện không thể lặp lại thì không có tính khoa học. Còn một khi chúng đã được tái lập, chắc chắn sẽ có một nguyên lý khoa học phía sau đó.
Vậy thì, thứ khoa học gì đã khiến những cốc cà phê hình "cái mông" được vẽ đi vẽ lại trên toàn thế giới?
Thậm chí chẳng cần phải là một barista hay một nhà khoa học, chính bạn cũng có thể vẽ ra một cái mông hoàn hảo trong cốc cà phê của mình – tự mình tái lập thí nghiệm đó để kiểm chứng khoa học.

Hóa ra, những cái mông này đều đã được tạo ra từ một trong những nguyên tắc cơ bản của vật lý, một bài toán đã 500 năm tuổi, thứ từng khiến bao thế hệ nhà khoa học phải đắm say - từ Galileo Galilei, Pierre de Fermat, René Descartes cho đến Marin Mersenne, Isaac Newton và Gottfried Wilhelm Leibniz…
Nhưng đừng lo, một lần nữa, bạn không cần phải là Isaac Newton hay René Descartes để hiểu về bài toán này. Vì nó đơn giản như là…

Tưởng tượng một chiếc xe đạp đang đi trên một đường thẳng, và ai đó gắn một chiếc van phát sáng cho nó. Chiếc van sẽ vạch vào không trung những cung tròn đều nhau gọi là cycloid.

Người đặt ra thuật ngữ này lần đầu tiên chính là Galileo Galilei, nhà bác học người Ý sống ở thế kỷ 16, nổi tiếng với câu nói: "Dù sao Trái Đất vẫn quay".
Galilei là một trong những người đầu tiên ủng hộ Thuyết Nhật tâm, cho rằng Trái Đất quay quanh Mặt Trời. Nhưng trước khi ông quan sát được chuyển động quay khổng lồ đó, Galilei đã tự hỏi một câu hỏi đơn giản hơn:
Điều gì sẽ xảy ra với chuyển động của một điểm, trên một đường tròn, khi nó lăn trên một đường thẳng?
Câu trả lời: Nó sẽ vạch ra những đường cong đều nhau mà Galilei đặt tên là "cycloid".

Sau khi phát hiện ra đường cycloid, Galilei ngay lập tức bị mê hoặc bởi nó. Ông muốn biết độ dài của nó là bao nhiêu, diện tích của nó, và thậm chí khối lượng của nó. Trên thực tế, Galilei đã chế tạo hẳn một tấm cycloid bằng kim loại để cân nó lên nhằm ước tính diện tích của cycloid một cách gián tiếp.
Mặc dù ý tưởng này của Galilei cuối cùng không đi tới thành công, nhưng đường cycloid của ông đã châm ngòi cho một trong những cuộc chạy đua toán học thú vị nhất trong thế kỷ 17 và 18. Gần như mọi nhà toán học ở Châu Âu đều bị ám ảnh bởi đường cycloid. Pierre de Fermat, René Descartes, Johannes Bernoulli, Isaac Newton và Gottfried Wilhelm Leibniz đều nghiên cứu về nó.
Thậm chí, cycloid còn đưa Blaise Pascal trở lại với toán học, người trước đó từng bị thần học mê hoặc và đã thề không bao giờ làm toán nữa.
Chuyện kể rằng một đêm nọ, Pascal bị đau răng kinh khủng khiếp. Ông không biết làm cách nào để xua tan cơn đau ngoài việc làm cho tâm trí mình bận rộn. Trong cơn bĩ cực đó, Pascal đã đặt ra rất nhiều bài toán liên quan đến đường cycloid.
Và kỳ diệu thay, trong khi suy nghĩ về những đường cong này, cơn đau răng của Pascal đã biến mất. Ông nghĩ rằng hẳn Chúa đã cho phép mình làm toán trở lại. Kể từ đó, Pascal không bao giờ ngừng nghiên cứu.

Có thể nói rằng nếu không có đường cycloid, nhân loại có lẽ đã vĩnh viễn mất đi một nhà khoa học đi vào con đường u mê của thần học. Nếu Pascal không thoát ra khỏi đó, chúng ta sẽ vĩnh viễn không có định luật Pascal, không có máy tính cơ học và quan trọng nhất là không có thuyết xác suất.
Mặc dù nó sẽ giúp bạn không phải trầy trật thi qua môn xác suất thống kê ở trường đại học, nhưng nếu Pascal không phát biểu thuyết xác suất, điều đó đồng nghĩa với các hệ thống bảo hiểm, đầu tư tài chính và kinh tế hiện nay sẽ sụp đổ. Không có Pascal cũng đồng nghĩa với không có máy tính và trí tuệ nhân tạo (AI) vì cả hai đều cần những nguyên lý cơ bản của toán xác suất.
Vai trò của Pascal lớn đến nỗi, Bảo tàng Louvre ở Paris đã trưng bày một bức tượng của ông đang ngắm nhìn một đường cong cycloid.

Khi Blaise Pascal bắt đầu nghiên cứu đường cycloid vào năm 1658, đó là một lĩnh vực tương đối mới đối với ông. Mặc dù vậy, Pascal chỉ mất vỏn vẹn vài tháng để giải được cùng lúc 3 bài toán, mà thế hệ đi trước ông như Galileo Galilei mất cả đời không tìm ra kết quả.
Các bài toán này bao gồm: tính diện tích của hình dưới cung cycloid, tìm thể tích của khối tròn xoay khi một cung cycloid quay quanh trục, xác định trọng tâm lực của các đoạn cycloid và các khối tạo ra bởi nó.
Vẻ đẹp của đường cycloid bây giờ bắt đầu hiện ra.

Nhìn bằng mắt thường, ngay cả Galilei cũng khó có thể hình dung được diện diện tích của một hình dưới cung cycloid sẽ bằng đúng 3 lần diện tích hình tròn lăn tạo ra nó. Chiều dài của một cung cycloid thì dễ nhận ra hơn, nó bằng đúng 8 lần bán kính của hình tròn lăn.
Nếu bán kính của hình tròn lăn là r, thể tích khối tròn xoay mà đường cycloid nó tạo ra bằng đúng 3π2r3, còn trọng tâm của cung cycloid sẽ nằm ở 4r/3 ngay chính giữa đường cao của nó.
Trong toán học, những con số tròn trĩnh này được gọi là cực kỳ "đẹp", đặc biệt là trong mối quan hệ phi trực quan giữa hình tròn lăn và đường cycloid mà nó tạo ra.
Hãy so sánh điều này với những con số "ít đẹp" hơn trong toán học. Chẳng hạn như độ dài của đường chéo một hình vuông gấp căn bậc 2 độ dài cạnh của nó, một số vô tỷ √2=1.414213562373... Chiều cao của một tam giác đều bằng một nửa căn bậc 3 chiều dài cạnh tam giác, nó cũng là một số vô tỷ √3/2= 0,86602540378…

Một phương pháp để tính diện tích hình dưới cung cycloid.
Sau khi tìm ra được vẻ đẹp của đường cycloid, Pascal đã tổ chức hẳn một cuộc thi vào tháng 6 năm 1658, thách thức tất cả các nhà toán học ở Châu Âu giải được cả ba bài toán liên quan đến đường cycloid giống như ông. Người nào giải được, Pascal sẽ theo thưởng 40 đồng vàng Tây Ban Nha.
Kết quả khi thời hạn của cuộc thi kết thúc vào tháng 10 năm 1658, chẳng một ai có thể giải được và Pascal tự trao giải thưởng cho chính mình. Điều này đã khiến một số người trong cộng đồng toán học chỉ trích Pascal là một kẻ ngạo mạn, vì ông tổ chức cuộc thi, chỉ với mục đích khẳng định tài năng cá nhân.
Nhưng những "drama" liên quan đến đường cycloid không chỉ dừng lại ở đó. Trước cuộc thi của Pascal, đường cong này cũng dính vào một loạt lùm xùm tranh chấp khoa học. Chuyện liên quan đến Gilles de Roberval, một nhà toán học người Pháp và là bạn của Pascal.
Roberval được biết đến là người đầu tiên tính ra được diện tích hình cycloid bằng một phương pháp như tích phân. Ông chia nhỏ đường cycloid thành vô hạn các đường cong nhỏ, tính các diện tích bên dưới chúng rồi cộng lại để nhận ra con số bằng đúng 3 lần diện tích hình tròn lăn.
Mặc dù vậy, Roberval không công bố kết quả của mình một cách rộng rãi mà chỉ khoe nó với một vài người bạn qua thư từ.

Sau đó 6 năm, Evangelista Torricelli, một nhà toán học người Ý, học trò của Galileo Galilei, cũng đã độc lập tính được diện tích của hình bên dưới cycloid. Nhưng lần này, ông công bố kết quả của mình một cách rộng rãi, khiến Roberval nổi đóa vì cho rằng Torricelli đã "đạo" ý tưởng của mình.
Torricelli không lâu sau đó qua đời vì bệnh thương hàn. Roberval nói rằng nhà toán học người Ý đã chết vì xấu hổ khi bị ông vạch trần. Nhưng sự thật không phải vậy, cả hai đều tính được diện tích cycloid một cách độc lập.

Tiếp tục mạch "drama" liên quan đến đường cycloid, lần này với sự tham gia của hai nhà toán học Johannes Bernoulli, người Thụy Sĩ và Isaac Newton, người mà chúng ta đã quá quen thuộc đến từ Vương Quốc Anh.
Vào tháng 6 năm 1696, Bernoulli sau khi tự giải được một bài toán gọi là đường cong Brachistochrone, đã công khai thách thức tất cả các nhà toán học trên khắp thế giới giải được nó giống như ông.
Có vẻ như vào thế kỷ 17, các nhà toán học cũng thích các thử thách "challenge" như chúng ta ngày nay trên mạng xã hội. Và "mạng xã hội" của các nhà khoa học trong thế kỷ 17 là Acta Eruditorum, một tạp chí khoa học tiếng Latin được xuất bản ở Châu Âu.

Brachistochrone trong tiếng Hy Lạp cổ nghĩa là "thời gian ngắn nhất". Bài toán này yêu cầu tìm một đường cong nối từ điểm A xuống điểm B nằm thấp hơn, sao cho khi một hạt trượt không ma sát dưới tác động của lực hấp dẫn, nó sẽ đi từ A đến B nhanh nhất.
"Tôi, Johann Bernoulli, xin gửi lời chào đến những nhà toán học lỗi lạc nhất thế giới. Tôi biết sẽ không có gì hấp dẫn được những người thông minh như các ngài hơn một bài toán chân thật, đầy thách thức và lời giải của nó sẽ mang lại danh tiếng như một tượng đài trường tồn.
Noi gương của những Pascal, Fermat…, tôi hi vọng sẽ nhận được lòng biết ơn của toàn thể cộng đồng khoa học, bằng cách đặt trước những nhà toán học lỗi lạc nhất của thời đại chúng ta một bài toán sẽ thử thách phương pháp và sức mạnh trí tuệ của họ.
Nếu ai gửi cho tôi lời giải của bài toán này, tôi sẽ công khai tuyên bố rằng người đó xứng đáng được ngợi khen", Bernoulli viết vào tháng 6 năm 1696.
Với sự phức tạp của bài toán Brachistochrone, Bernoulli – người đã mất 2 tuần để giải nó- tự tin đặt thời hạn chót cho thử thách là 6 tháng. Sau đó, ông còn gia hạn nó lên 1,5 năm theo lời gợi ý của nhà toán học người Đức Gottfried Leibniz, đồng sáng lập tạp chí Acta Eruditorum.
Thế nhưng, điều mà cả hai nhà toán học ở Châu Âu đã không lường trước được là bên kia eo biển Anh, có một người chỉ mất vỏn vẹn 1 đêm để giải quyết nó. Không ai khác, đó chính là Isaac Newton.

Chuyện kể rằng vào một buổi chiều tháng 1 năm 1697, Newton trở về nhà từ Xưởng Đúc tiền Hoàng gia Anh thì thấy có một lá thư trên bàn gửi cho mình. Nó là thư của Johann Bernoulli kèm với lời thách thức của bài toán Brachistochrone.
Có lẽ nhà toán học người Thụy Sĩ đã gửi riêng lá thư này cho Newton, vì sau hơn 6 tháng không thấy ông tham gia vào thử thách của mình trên tạp chí Acta Eruditorum. Trên thực tế, đó là khoảng thời gian mà Newton đã không còn mặn mà với công việc học thuật.
Ngoài 50 tuổi, ông gần như đã nghỉ hưu khỏi toán học và vật lý. Newton rời Đại học Cambridge đến Xưởng Đúc tiền Hoàng gia Anh để nhận một công việc được coi là an nhàn cho tuổi trung niên của mình.
Tại đây, Newton phụ trách việc thiết kế tiền xu cho Hoàng Gia Anh để tăng độ chính xác, tránh cho chúng khỏi bị làm giả. Ông cũng tự mình hóa trang thành thám tử, đi bắt những kẻ đúc tiền giả, thẩm vấn và trừng phạt chúng, một tội được coi là phản quốc và phải bị treo cổ.
Thế nhưng vào buổi chiều hôm đó, sau một ngày làm việc vất vả ở xưởng đúc tiền, Newton thấy lá thư từ Johann Bernoulli thì lại thấy "ngứa nghề". Ông đã ngồi xuống và giải quyết nó chỉ trong vòng 1 đêm.

Bằng phương pháp vi tích phân mà chính mình phát triển, Newton đã tìm ra đường cong Brachistochrone nhanh nhất chính là đường cycloid. Ông sau đó đã gửi lời giải của mình cho Bernoulli.
Điều thú vị là dù Newton chỉ gửi thư ẩn danh, Bernoulli cũng biết đó là đáp án của ai. "Tôi có thể nhận ra con sư tử từ móng vuốt của nó", Bernoulli nói.
Còn Newton bình luận về sự việc này: "Tôi không thích bị những người ngoại quốc trêu tức và làm phiền về những gì liên quan đến toán học". Trên thực tế, Newton không ưa những nhà toán học ở Châu Âu Đại lục thời đó, bao gồm Leibniz, người sáng lập tạp chí Acta Eruditorum đã đăng bài toán của Bernoulli, và cũng là người tranh chấp phát minh phép tính vi phân với ông.
Vậy đường cycloid còn là tâm điểm của những drama toán học nào? Nó còn có những tính chất kỳ diệu và ứng dụng đột phá nào khác nữa? Rốt cuộc, bạn có thể tạo ra hình cái mông trong tách cà phê bằng công thức nào? Mời độc giả đón đọc kỳ tiếp theo của bài viết:
500 năm diệu kỳ của vật lý và toán học, hội tụ trong một cốc cà phê hình "cái mông": Những đường cong đóng lõi lò phản ứng hạt nhân, mở ra nhịp sống mới
Thanh Long
